Linear Search in Python

What is Searching Algorithm?

A searching algorithm is designed to find an element or object from a collection of elements or objects with a given data structure. For example, search the minimum height from a given a list of heights, or search for the highest mark from a list or array of numbers. Few popular searching algorithms include “Linear Search”, “Binary Search”, “Jump Search”, “Fibonacci Search,” etc.

What is Linear Search?

Linear search is one of the simplest search algorithms. From a given list or array, it searches for the given element one by one. Linear Search iterates over the whole list and checks if any particular element is equal to the search element. It’s also called the sequential search.

What does Linear Search Function do?

An array of integers is given as “Numbers,” and a variable “item” contains the integer number to search.

Now, the Linear Search algorithm can provide the following output:

• “-1”; this means that the given element is not found in the array
• Any number between 0 to n-1; means that the search element is found, and it returns the index of the element on the array. Here, “n” represents the size of the array.

How does Linear Search work?

Let’s say an array containing integer numbers. The task is to find a given number in the array.

• If the number is located in the array, we need to return the index of that number.
• If the given number is not found, then it will return -1.

In the flowchart, “Data” is the integer array, “N” is the size of the array, and the “item” is the number we want to search in the array.

Flowchart for Linear Search Algorithm:

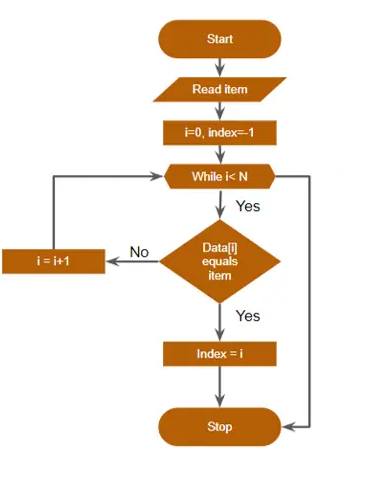
Here are the steps of the flowchart:

Step 1) Read the search item, “item.”

Step 2) Initiate i=0 and index=-1

Step 3) If i<N, go to step 4. Else, go to step 8.

Step 4) If Data[i] equals to “item,” then go to step 5. Else go to step 6.

Step 5) Index = i (As the item is found at index no i). Go to step 8.

Step 6) i = i +1.

Step 7) Go to step 3.

Step 8) Stop.

For simplicity, we provide an example with an array of integers. Linear search is also applicable in the string, an array of objects, or struct.

Pseudo Code for Sequential Search Algorithm

function linearSearch: in →Data[], item
foundAt = -1
for i in (0 to data.length): if data[i] equals item
// item is found in the array
// returning the index
return i
// item not found in the array
// -1 means no item found, as negative index is not valid
return -1

C++ Code Example Linear Search

#include < bits / stdc++.h >
    using namespace std;
int linearSearch(int * arr, int item, int n) {
    int idx = -1;
    for (int i = 0; i < n; i++) {
        if (arr[i] == item) {
            idx = i;
            break;
        }
    }
    return idx;
}
int main() {
    int array[] = {
        1, 9, 8, 7, 6, 3, 11, 4, 6, 9, 7, 2, 0, 19, -10
    };
    int n = sizeof(array) / sizeof(arr[0]);
    int item;
    cout << "Enter a number to search: ";
    cin >> item;
    int idx = linearSearch(arr, item, n);
    if (idx >= 0) {
        cout << item << " is found at index " << idx << endl;
    } else {
        cout << "Could not find " << item << " in the array" << endl;
    }
}

Output:

Enter a number to search: -10
-10 is found at index 14

Python Code Example Linear Search

def linearSearch(data, item):
    for i in range(len(data)):
    if data[i] == item:
    return i
return -1
data = [1, 9, 8, 7, 6, 3, 11, 4, 6, 9, 7, 2, 0, 19, -10]
item = int(input("Enter a number to search: "))
idx = linearSearch(data, item)
if idx >= 0:
    print("{} is found at index {}".format(item, idx))
else :
    print("{} was not found".format(item))

Output:

Enter a number to search: -10
-10 is found at index 14

Complexity Analysis of Linear Search Algorithm

Generally, time complexity means, the amount of CPU time to perform a certain task. In the linear search algorithm, the task is to find the search key from the element of the array.

Three types of time complexities are:

• Worst Case Scenario
• Best Case Scenario
• Average Case Scenario

Time Complexity of linear search in Worst-Case Scenario:

Let’s say, we need to perform a linear search in an array with a size of “n”. We can find the search item between index 0 to n-1. Worst-case scenario, the algorithm will try to match all the elements from the array with the search element.

In that case, the worst-case complexity will be O(n). Here, “O”-big O Notation means the complexity function.

Time Complexity of linear search in Best-Case Scenario:

Let’s say we are searching for an element that resides in the first position at the array. In this scenario, the linear search algorithm won’t search for all n elements in the array. So the complexity will be O(1). This means constant time.

Time Complexity of linear search in average case scenario:

When an element is found at the middle index of the array, then it can be said that the average case complexity for linear search is O(N), where N means the length of the array.

The space complexity of the linear search algorithm

Space complexity for the linear search is always O(N) because we don’t need to store or use any kind of temporary variable in the linear search function.

How to improve Linear Search Algorithm

Search can be done multiple times throughout the program’s lifecycle. It’s also possible that we are running the linear search algorithm and searching for any specific key several times. We can use the “Binary Search Algorithm” if the array is a sorted array.

Assume that the array consists of 10 thousand numbers, and the target element is found at the 5000th index. So, the algorithm will try to compare 5000 elements. Now, comparisons are CPU-heavy tasks. To optimize the linear search algorithm, we have two options.

• Transposition
• Move to Front

Transposition:

In this method, we will swap the search element with its previous element in the array. For example, let’s say you have an array like the following:

Data[] = {1,5,9,8,7,3,4,11}

Now, we want to search 4. Steps of Transposition:

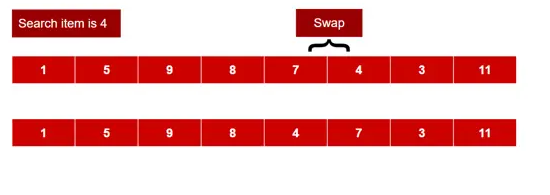
Step 1) “4” is found at index 6. It took six comparisons.

Step 2) Swap data[6] and data[5]. Then the data array will look like:

Data[] = {1,5,9,8,7,4,3,11}

Step 3) Search 4 again. Found at index 5. This time it took five comparisons.

Step 4) Swap data [5] and data[4]. Then the data array will look like this:

Data [] = {1,5,9,8,4,7,3,11}

Now, if you notice, the more frequent a key is being searched, the more it decreases the index. Thus, decreasing the number of comparisons.

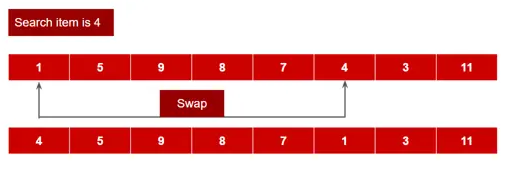
Move to the front:

In this method, we swap the search element in the 0th index. Because if it’s searched again, we can find it at O(1) time.

Application of Linear Search Algorithm

Here are some linear search applications we can use.

• For small-sized arrays or only a few elements in the list, it’s easier to use linear search.
• Linear search method can be used in single or multi-dimensional arrays or other data structures.
• Generally, linear search is simple and efficient to perform a search in the “unordered” data. We can fetch a single data from the given unordered list easily.